Im Unternehmen fokussiert man sich schnell auf Plot-Libraries, um z.B. Daten, Prognosen, Graphen, Abläufe oder Korrelationen zu visualisieren. Es gibt Dutzende davon (JSXGraph, Plotta.js, JSPlot, Plotly.js, Highcharts, D3.js, C3.js, Chart.js, usw.). Doch im Grunde will man doch nur einen einfachen Plot darstellen. Was aber, wenn im weiteren Verlauf spezielle Plots benötigt werden? Was soll man machen, wenn die Plot-Library eine spezielle Einstellung nicht unterstützt?
In diesem Artikel möchte ich zeigen, wie man mit wenig Code Plots selber schreiben kann und damit die Möglichkeit besteht, die individuellen Bedürfnisse voll zu entfalten.
Visualisierungen mit HTML Canvas erstellen
In meinem Studium habe ich bei dem Uni-Projekt math4u2 mitgearbeitet, welches mathematische Sachverhalten visuell beschreibt. Dabei entstand eine Reihe von Darstellungskomponenten, die auch hier öffentlich erreichbar ist. Leider ist alles in Java-Swing geschrieben und wird nicht mehr weiter entwickelt. Diese Komponenten sind für mich in vielen Situationen sehr praktisch. Besonders nützlich sind dabei folgende Komponenten:
- Zeichenfläche mit einer Gitterdarstellung
- Darstellung von 2D-Funktionen (Funktion mit einer Variable)
- Darstellung von 3D-Funktionen (Funktion mit zwei Variablen) mittels einer Heatmap (bzw. Farbiger Contour-Plot)
- Darstellung von parametrisierten Kurven
- Darstellung von Richtungsfeldern
Mit diesen Komponenten besitzt man einen Grundstock von simplen Visualisierungen und kann einfach und modular spezielle Visualisierungen erstellen. Auch die Interaktivität ist ohne viel Aufwand durchzuführen, indem die Canvas mit den neuen Parametern neu gerendert wird.
Immer, wenn ich einen neuen Algorithmus oder eine spezielle Visualisierung im Kopf hatte, habe ich mich auf die Suche nach einer HTML-Library gemacht, die einen ähnlichen Funktionsumfang hat. Leider bin ich bis heute nicht fündig geworden.
Beispielsweise finde ich folgende Visualisierungen nützlich:
Evaluierungspunkte einer 3D-Funktion
Lage und Richtung von Partikeln auf einer 3D-Funktion
Historie einer Suche
Histogram im unteren Bereich der Funktionsevaluierungen
Vor einiger Zeit wollte ich wieder einen Algorithmus visualisieren und habe mich schlussendlich entschieden, die wichtigsten Teile von math4u2 auf HTML Canvas zu überführen.
Ich habe HTML Canvas bereits verwendet, um gut komprimierte Bilder mit Alpha-Kanal zu rendern, da das PNG-Format in unserem Projekt zu schlechte Kompressionsraten hatte und wir Tools wie TinyPNG nicht verwenden wollten. Dabei wurde das eigentliche Bild als JPG-Bild und der Alpha-Kanal als weiteres JPG-Graustufenbild übertragen. Im HTML Canvas wurden beide Bilder kombiniert.
HTML Canvas hat ähnliche Konzepte wie die Swing Canvas, und Überführung war deswegen nicht besonders schwierig. Die Zeichenfläche, sowie 2D- und 3D-Funktionen, konnte ich mit nur 200 JavaScript-Zeilen aufbauen. Ich werde im Weiteren beschreiben, wie man selbst schnell und einfach eigene Visualisierungen erstellt. Der aktuelle Stand kann unter https://github.com/fennstef/graphplot betrachtet werden.
Gitter der Zeichenfläche
Zuerst soll ein Gitter für die Zeichenfläche gezeichnet werden. Die Verwendung ist relativ einfach.
Wir beginnen mit der Festlegung einer Canvas. Danach wird der JavaScript-Code geladen, der später im einzelnen durchgegangen wird. Alle Konfigurationen werden als ein Javascript Object – kurz Config-Map genannt – abgelegt.
- xMin, xMax, yMin, yMax legen den Bereich der Zeichenfläche fest.
- Ctx ist der Canvas-Context und wird für die Berechnung und das Zeichnen benötigt.
Zum Schluss wird die drawGrid-Funktion aufgerufen, welche das Gitter auf die Canvas zeichnet.
Um ein Gitter einzuzeichnen, sind folgende Berechnungen jeweils für die X- und Y-Richtung durchzuführen:
Berechnung der Gitterdistanz
Die Gitterdistanz wird abhängig von dem Definitionsbereich (diff) mit einer möglichst guten Passung (nicht zu viele und nicht zu wenige Gitterlinien) berechnet.
Die Formel in der dritten Zeile findet die richtige 10er Potenz für die Gitterdarstellung.
Beispiel 1 mit diff=5: Math.pow(10.0, Math.ceil(Math.log(5) / Math.log(10.0)) – 1) = Math.pow(10.0, Math.ceil(0.69) – 1) = Math.pow(10.0, 1 – 1) = Math.pow(10.0, 0) = 1
Ergebnis: Bei einem Bereich von z.B. [0..5] werden an jeder ganzen Zahl die Gitterlinien eingezeichnet.
Beispiel 2 mit diff=11: Math.pow(10.0, Math.ceil(Math.log(11) / Math.log(10.0)) – 1) = Math.pow(10.0, Math.ceil(1.04) – 1) = Math.pow(10.0, 2 – 1) = Math.pow(10.0, 1) = 10
Ergebnis: Bei einem Bereich von z.B. [0..11] werden an jeder ganzen 10er-Einheit die Gitterlinien eingezeichnet.
Beispiel 2 würde dann aber nur eine Gitterlinie erhalten. Das zeigt, dass der Sprung von 1er Einheiten zu 10er Einheiten zu groß ist. Deshalb wird im switch bei “wenigen Gitterelementen” die Anzahl erhöht. Dabei werden nur Brüche mit kurzer Dezimaldarstellung verwendet (0.5, 0.25, 0.2). Mit der Variablen “factor” kann die Feinmaschigkeit des Gitters noch weiter justiert werden.
Berechnung der ersten Gitterlinie
Die erste Gitterlinie ist die Gitterlinie, die dem Minimalwert des Bereichs am nächsten steht.
startValue = Math.ceil(min / gridDist) * gridDist
Dabei wird mit der “Einheit” gridDist geteilt, dann aufgerundet und wieder mit gridDist multipliziert. Im Beispiel 1 mit dem Bereich [1.2 … 6.2] ergibt die Rechnung: Math.ceil(1.2 / 1) * 1 = 2. Also wird die erste Gitterlinie bei 2 eingezeichnet.
Mit diesen beiden Werten kann man nun relativ einfach ein Gitter aufbauen.
Beispiel Gitter der Zeichenfläche:
Folgende Canvas Draw-Funktionen werden dabei verwendet:
- clearRect: Setzt den ausgezeichneten Bereich zurück, d.h. der Bereich wird gelöscht.
- fillText: Zeichnen der Gitterlinien-Beschriftung.
- beginPath, moveTo, lineTo, stroke: Zeichnet einen Pfad; hier wird nur eine einfache Linie gezeichnet.
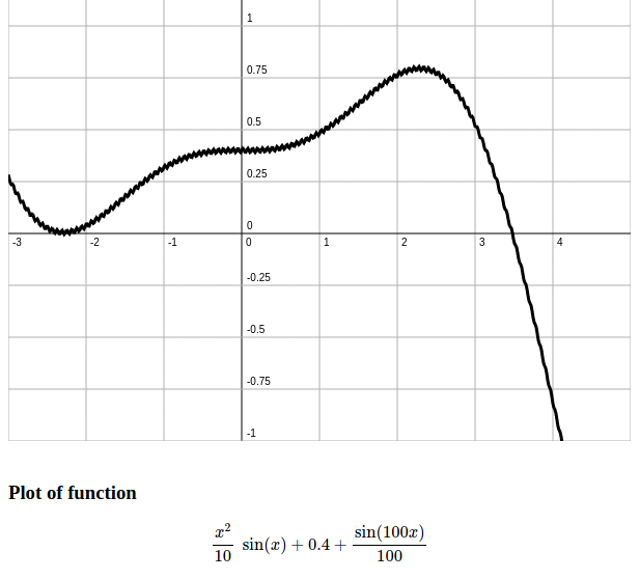
2D-Funktionen
Um eine 2D-Funktion — also eine Funktion mit einer Variable — zu zeichnen, ist lediglich die drawFunction-Funktion aufzurufen. Trotzdem ist ein gewisses Setup nötig. Um im Canvas mit verschiedenen Ebenen zu arbeiten, und nicht alles immer wieder neu zeichnen zu müssen, werden mehrere HTML Canvases mit gleicher Größer übereinander gelagert. Dies wird direkt mit CSS position:absolute erledigt.
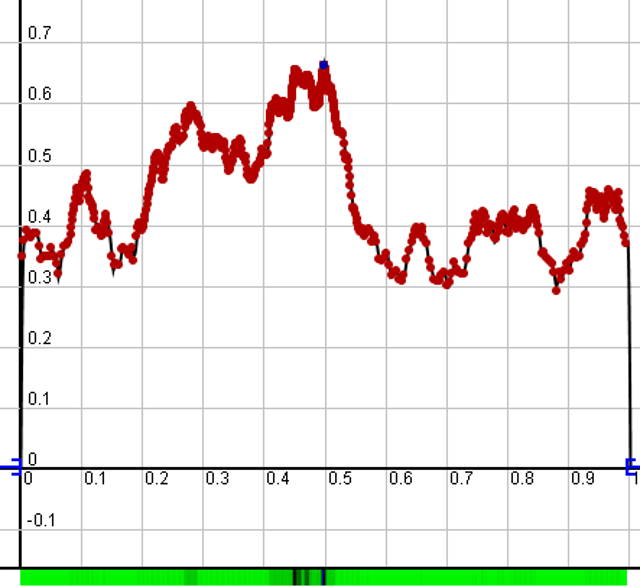
Beispiel 2D-Funktion:
Die drawFunction-Funktion erhält als Parameter den Canvas-Kontext der Ebene, die Graph-Farbe und die Funktion in Form eines Lambda-Ausdrucks. Die Konfiguration configF2 wird von config bis auf den Canvas-Kontext kopiert. Die drawFunction-Funktion ist relativ einfach.
Zuerst wird der Canvas komplett zurückgesetzt und die Zeichnen-Eigenschaft Stroke festgelegt. Danach wird für jeden x-Pixel-Wert — hier w für width — mit xPixToCoord die x-Koordinate berechnet. Analog existieren die Funktionen xCoordToPix, yPixToCoord, yCoordToPix, und diese Funktionen sind der Dreh- und Angelpunkt für alle selbsterstellten Plots. Danach wird die Funktion aufgerufen, und man erhält den y-Koordinaten-Wert. Nun wird y in den y-Pixel-Wert — hier h für height — umgerechnet. Ist es der erste Punkt, so wird als Pfad-Operation moveTo verwendet, ansonsten lineTo.
Natürlich kann man noch ausgefeiltere Zeichenmethoden erstellen. Beispielsweise sollte bei Polen keine Linie gezeichnet werden. Außerdem könnte man nur jeden fünften Punkt evaluieren und mit quadraticCurveTo einen glatten Übergang einzeichnen.
3D-Funktionen
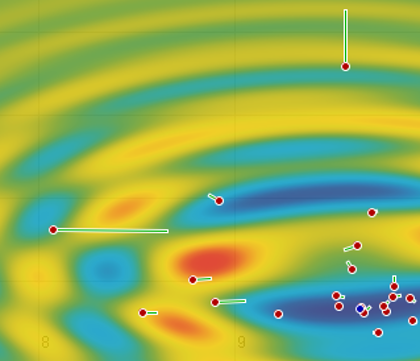
3D-Funktionen — also eine Funktion mit zwei Variablen — werden in der Regel als dreidimensionale Oberfläche dargestellt. Für viele Anwendungsfälle ist dies unzureichend, da z.B. die Anreicherung/Überlagerung von weiteren Plots schwierig ist. Auch kann ein “Gebirge” wichtige Aspekte verbergen.
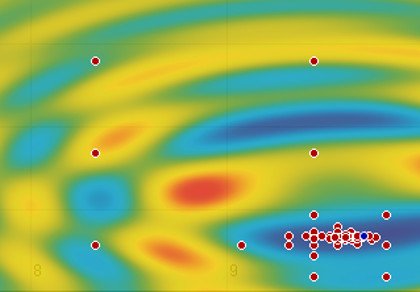
Deshalb bevorzuge ich in der Regel ein Heatmap-Diagramm. Dabei wird für jede Punkt (x,y) der Funktionswert z berechnet. Der z-Wert wird anhand eines Gradientenverlaufs eingefärbt, und es entsteht die Farbkarte der Funktion. Um zMin und zMax zu bestimmen, müssten alle Punkte der Karte bereits evaluiert worden sein. Da dies in der Regel nicht möglich ist, muss beim Plotten der Heatmap der zMin– und zMax-Wert angegeben werden. Falls ein Funktionswert oberhalb oder unterhalb der Grenzen liegt, wird der Farbwert mit erhöhter Transparenz eingezeichnet.
Gradient
Heatmap der Funktion
Obwohl hier dreimal die gleiche Funktion abgebildet wird, entstehen durch den Farbverlauf unterschiedliche Bilder. Im ersten Bild ist der Höhenverlauf sehr gut wiedergegeben, und der Fokus liegt auf vier Bereiche: Blau, Grün, Gelb und Rot. Im zweiten Bild konzentriert man sich mehr auf die besonders dunklen und türkisen Bereiche. Im dritten Bild bekommt man einen Eindruck von den Höhenlinien der Funktion.
Erzeugung des Gradienten
Für einen Gradienten werden für bestimmte Positionen zwischen 0 und 1 die Farbwerte hinterlegt. Der Schwarz-Türkise Gradient ist wie folgt beschrieben.
Anhand dieser Angaben (im Code als ‘gradientColors[pos]’ bezeichnet) kann der Gradient auf ein Hilfs-Canvas mit der Auflösung 1 x levels gezeichnet werden.
Dabei wird ein neuer Canvas gezeichnet und die Bilddaten als Array zurückgegeben.
Plot eines Pixels
Wenn die aktuelle Pixelposition mit Koordinate (w, h) eingezeichnet wird, wird der Funktionswert berechnet, der entsprechende Gradientenfarbwert bestimmt und im Image-Data Array eingetragen (dabei ist ‘c’ die Config-Map).
In der ersten Zeile wird der z-Wert bestimmt. Der Gradienten-Array beinhaltet für jedes Pixel immer die RGBA-Werte. Da das Bild nur eine Höhe von 1 hat, kann die Breite mit Länge/4 berechnet werden.
Danach wird z aus den Bereich [zMin, zMax] in den Bereich [0;pixelCount-1] transformiert. Aus dem gradientIndex wird die RGBA-Gradiententfarbe ermittelt.
Der Alpha-Wert wird angepasst, falls sich z außerhalb des Bereichs befindet, und schließlich wird der Farbwert auf den Image-Array des Canvas eingetragen. Auch hier muss für (w, h) die richtige Array-Position berechnet werden.
Höhenlinien kann man hier auch relativ einfach einzeichnen, indem man für festgelegte z-Werte inklusive eines kleinen Einzugsbereiches die Höhenlinie-Farbe verwendet.
Plot der Heatmap
Mit einem naiven Ansatz würde man nun mit zwei For-Schleifen alle Pixelwerte durchlaufen und berechnen. Leider stockt bzw. hängt damit das Rendern der restlichen Seite bei der Berechnung von aufwändigen Funktionen. Deshalb wird der Ablauf nach einer Zeitspanne abgebrochen und mit setTimeout später wieder fortgesetzt. Der Zustand des Berechnungsfortschritt wird mit der aktuellen Position (w, h) im Bild gespeichert.
Zu Beginn wird die Zeichenfläche gelöscht, der Image-Array erstellt und w, h initialisiert. In ‘drawInTimeSlot’ wird die while-Schleife durchlaufen, solange keine 70ms verstrichen sind. In der while-Schleife wird entsprechend w und h inkrementiert und das einzelne Pixel gezeichnet. Nach der while-Schleife, wird der aktuelle Stand auf dem Canvas eingezeichnet, und falls noch nicht alles berechnet wurde, wird die Funktion drawInTimeSlot mittel setTimeout zeitversetzt aufgerufen.
Fazit
HTML Canvas ist für alle pixelgenauen Aufgaben bestens geeignet. Bei meiner Arbeit mit HTML Canvas waren nur wenige Stolpersteine vorhanden, und es gibt genügend Beispiel-Code, um schnell die eigenen Ideen umzusetzen.
Die Darstellungskomponenten Gitter, 2D-Funktion und Heatmap sind ein gutes Fundament, um darauf basierend eigene Plots zu erstellen. Ich bin der Meinung, dass man erst mit der richtigen Visualisierung ein echtes Verständnis für die betrachtete Domäne bekommt. Beispielsweise habe ich erst bei dem Verlauf eines Optimierungsalgorithmus einen Fehler bei einer bestimmten Konstellation entdeckt, auf die ich sonst wohl nur sehr schwer gestossen wäre.
Ich hoffe, dass es in Zukunft mehr Plot-Libraries gibt, die es erlauben, einfach eigene Plots und Interaktivität zu integrieren. Das Projekt math4u2 wurde in einem c’t-Artikel als Anwendung mit “liebevoll gestalteten interaktiven Mathe-Lektionen” beschrieben, und ich würde mich sehr freuen, wenn math4u2 oder ein äquivalentes Projekt im Web dem interessierten User die Welt der Mathematik, Physik, Numerik, Data Science und Algorithmen näherbringt.
Daneben kann für viele Desktop-Applikationen mit “selbstgeschriebenen” Darstellungen die Verwendung von HTML Canvas der Sprung zur Web-App bedeuten, da hierfür die Web-Umstellung in relativ kurzer Zeit möglich ist.
Aufgrund seiner hohen Ansprüche an Softwarequalität und seinem Fachwissen über langlebige Softwarearchitekturen ist er bei der WOGRA seit 2016 der Hauptverantwortliche für die technische Umsetzung von Softwareentwicklungsprojekten (Chief Software Architect).
